
Zadanie Autostrady (aut)
Pomóż nam usprawnić bazę zadań!
Autostrady
Limit pamięci: 32 MB
Bajtocja posiada rozbudowaną sieć autostrad. Każda
autostrada łączy dwa miasta. Autostrady są płatne. Cena za przejazd autostradą zmienia się codziennie i może być różna
w różne strony. Koszt przejazdu autostradą (w każdym kierunku)
zmienia się liniowo. Inaczej mówiąc, istnieje stała 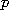 (zależna od
autostrady i kierunku) taka,
że każdego następnego dnia cena zmienia się o
(zależna od
autostrady i kierunku) taka,
że każdego następnego dnia cena zmienia się o 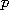 (stała
(stała 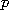 może być
ujemna, wtedy cena maleje, lub równa 0, wtedy cena nie zmienia się, lub
może być
ujemna, wtedy cena maleje, lub równa 0, wtedy cena nie zmienia się, lub 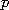 może być dodatnie, wtedy cena rośnie).
Zmiana cen przejazdu autostradami następuje o północy.
może być dodatnie, wtedy cena rośnie).
Zmiana cen przejazdu autostradami następuje o północy.
Bajtazar mieszka w mieście  . Pragnie odwiedzić znajomego, który mieszka w
mieście
. Pragnie odwiedzić znajomego, który mieszka w
mieście 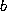 . Chce więc przejechać z miasta
. Chce więc przejechać z miasta  do
do  i wrócić tego samego
dnia do miasta
i wrócić tego samego
dnia do miasta  . Ponieważ jest oszczędny, to wybierze taki dzień, w
którym będzie mógł jak najmniej zapłacić za przejazd autostradami. Musi
jednak odwiedzić znajomego nie później niż dnia
. Ponieważ jest oszczędny, to wybierze taki dzień, w
którym będzie mógł jak najmniej zapłacić za przejazd autostradami. Musi
jednak odwiedzić znajomego nie później niż dnia  .
.
Sieć autostrad w Bajtocji jest na tyle rozbudowana, że z każdego miasta daje się dojechać do każdego innego.
Pomiędzy każdymi dwoma miastami jest najwyżej jedno bezpośrednie połączenie.
Bajtocja jest na tyle mała, że Bajtazar spokojnie zdąży przejechać do miasta 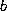 i
z powrotem w ciągu jednego dnia najtańszą trasą.
Ponadto wiadomo, że w
ciągu badanych
i
z powrotem w ciągu jednego dnia najtańszą trasą.
Ponadto wiadomo, że w
ciągu badanych  dni cena przejazdu każdą autostradą będzie dodatnia.
dni cena przejazdu każdą autostradą będzie dodatnia.
Zadanie
Napisz program, który:
- wczyta opis sieci autostrad, numery miast
 i
i 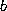 oraz liczbę dni
oraz liczbę dni  ,
,
- wyznaczy minimalny koszt przejazdu z
 do
do  i z powrotem w ciągu jednego spośród
i z powrotem w ciągu jednego spośród  pierwszych dni,
pierwszych dni,
- wypisze obliczony koszt.
Wejście
W pierwszym wierszu wejścia znajduje się pięć liczb całkowitych 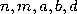 ,
, 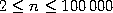 ,
,
 ,
,  , gdzie
, gdzie  jest liczbą miast,
jest liczbą miast, 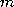 liczbą autostrad,
liczbą autostrad,  numerem miasta,
w którym mieszka Bajtazar,
numerem miasta,
w którym mieszka Bajtazar, 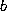 numerem miasta, w którym mieszka jego znajomy,
numerem miasta, w którym mieszka jego znajomy,  liczbą dni, w przeciągu których Bajtazar musi odwiedzić znajomego.
Miasta są ponumerowane od
liczbą dni, w przeciągu których Bajtazar musi odwiedzić znajomego.
Miasta są ponumerowane od 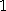 do
do  .
Możesz założyć, że Bajtazar mieszka w innym mieście niż jego znajomy.
W następnych
.
Możesz założyć, że Bajtazar mieszka w innym mieście niż jego znajomy.
W następnych 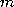 wierszach znajdują się opisy kolejnych autostrad. Każdy wiersz zawiera sześć liczb całkowitych:
wierszach znajdują się opisy kolejnych autostrad. Każdy wiersz zawiera sześć liczb całkowitych:
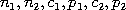 . Liczby
. Liczby 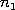 i
i 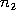 to numery miast, które łączy autostrada.
Liczby
to numery miast, które łączy autostrada.
Liczby 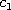 i
i 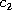 oznaczają ceny przejazdu z miasta
oznaczają ceny przejazdu z miasta 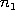 do
do 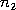 oraz z
oraz z 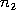 do
do 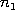 pierwszego dnia.
Każdego kolejnego dnia pierwsza z tych cen zmienia się o
pierwszego dnia.
Każdego kolejnego dnia pierwsza z tych cen zmienia się o 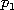 , a druga o
, a druga o 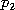 . Wiadomo, że podczas dni od
. Wiadomo, że podczas dni od
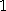 do
do  każda cena będzie dodatnia i nie większa niż
każda cena będzie dodatnia i nie większa niż 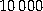 .
.
Wyjście
W pierwszym i jedynym wierszu powinna się znajdować dokładnie
jedna liczba całkowita - minimalny koszt dojechania z miasta  do
do  i z powrotem, w ciągu jednego z pierwszych
i z powrotem, w ciągu jednego z pierwszych  dni.
dni.
Przykład
Dla danych wejściowych:4 4 1 4 3 1 2 5 -1 10 -1 3 2 12 2 7 2 3 4 8 -1 20 -3 1 4 27 -2 3 0poprawną odpowiedzią jest:
23

Na powyższym rysunku jedno połączenie między dwoma miastami narysowane jest jako
para krawędzi, aby rozróżnić koszty w poszczególnych kierunkach. Para liczb przy każdej krawędzi
oznacza odpowiednio koszt pierwszego dnia, oraz zmianę kosztu jaka następuje po każdym dniu.
Jednym z optymalnych rozwiązań dla testu przykładowego jest przejechanie drugiego dnia trasy:
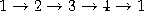 kiedy koszt przejazdu wynosi
kiedy koszt przejazdu wynosi 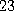 .
.
Autor zadania: Paweł Parys.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English